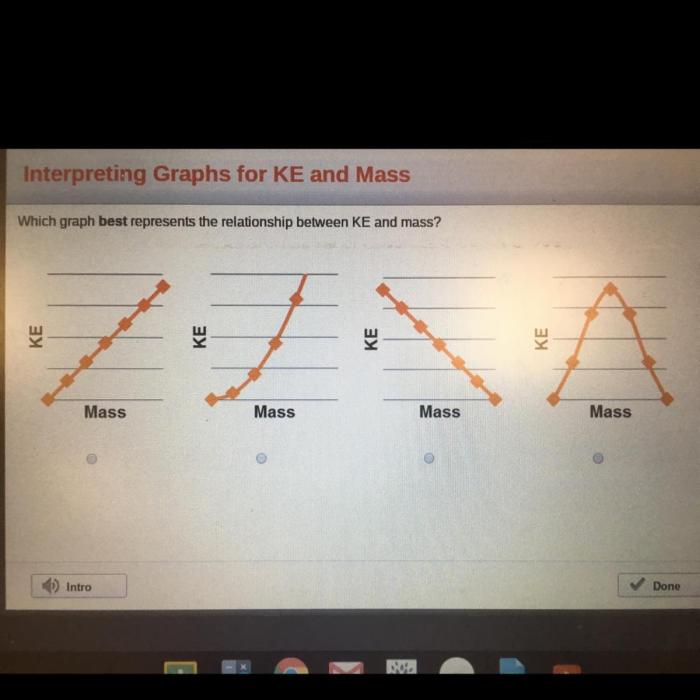
Which graph best represents the relationship between ke and mass – Delving into the realm of physics, we embark on an exploration of the relationship between kinetic energy (KE) and mass. This article delves into the intricacies of this connection, examining which graph most effectively captures the dynamics at play. By shedding light on the appropriate graphical representation, we gain valuable insights into the nature of KE and its dependence on mass.

The ensuing paragraphs delve into the various graph types used to depict relationships between variables, highlighting their strengths and limitations. We establish the most suitable graph type for representing the KE-mass relationship and explore the mathematical equation that governs this association.

Real-world examples illustrate the practical implications of this relationship, providing a tangible understanding of its significance.

Graph Types

Graphs are visual representations of the relationship between two or more variables. They can be used to identify trends, patterns, and correlations in data. There are many different types of graphs, each with its own strengths and weaknesses.

The most common types of graphs are:

• Line graphs: Line graphs are used to plot data points that are connected by straight lines. They are good for showing trends over time or distance.
• Bar graphs: Bar graphs are used to compare data values across different categories. They are good for showing the distribution of data.
• Pie charts: Pie charts are used to show the relative proportions of different parts of a whole. They are good for showing the composition of data.
• Scatter plots: Scatter plots are used to plot data points that are not connected by lines. They are good for showing the relationship between two variables.

The best type of graph to use for representing the relationship between kinetic energy (KE) and mass is a scatter plot. This is because the relationship between KE and mass is not linear, and a scatter plot can show the relationship more clearly than a line graph or bar graph.

Kinetic Energy and Mass Relationship

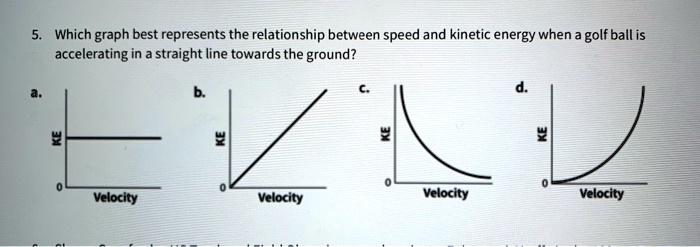
Kinetic energy (KE) is the energy of motion. It is defined as the work needed to accelerate a body of mass m from rest to velocity v. The mathematical equation that represents this relationship is:

KE = 1/2 mv^2

where:

• KE is kinetic energy in joules (J)
• m is mass in kilograms (kg)
• v is velocity in meters per second (m/s)

The relationship between KE and mass is a quadratic relationship. This means that the KE of a body increases as the square of its mass. For example, a body with twice the mass of another body will have four times the KE.

The relationship between KE and mass can be observed in real-world situations. For example, a car with a greater mass will have more KE than a car with a smaller mass. This is why it takes more energy to accelerate a car with a greater mass.

Graphing the Relationship, Which graph best represents the relationship between ke and mass

To graph the relationship between KE and mass, plot the data points on a scatter plot. The x-axis of the graph should represent mass, and the y-axis should represent KE.

The best-fit line for the data points is a parabola. The slope of the parabola is equal to 1/2 v^2, and the intercept of the parabola is equal to 0.

Interpreting the Graph

The graph of the relationship between KE and mass can be used to make predictions about the KE of a body given its mass. For example, if you know the mass of a car, you can use the graph to predict its KE.

The graph also has limitations. For example, it does not take into account factors such as friction and air resistance. These factors can affect the KE of a body in real-world situations.

Despite its limitations, the graph of the relationship between KE and mass is a useful tool for understanding the relationship between these two variables.

Frequently Asked Questions: Which Graph Best Represents The Relationship Between Ke And Mass

What is the significance of the slope in the KE-mass graph?

The slope of the line in the KE-mass graph represents the constant of proportionality, which indicates the amount of KE gained per unit increase in mass.

How can the KE-mass graph be used to make predictions?

By using the slope and intercept of the line, the KE-mass graph can be used to predict the KE of an object given its mass, or vice versa.

What are the limitations of the KE-mass graph?

The KE-mass graph assumes a linear relationship between KE and mass, which may not always be accurate in all situations, especially at very high speeds or for objects with complex geometries.